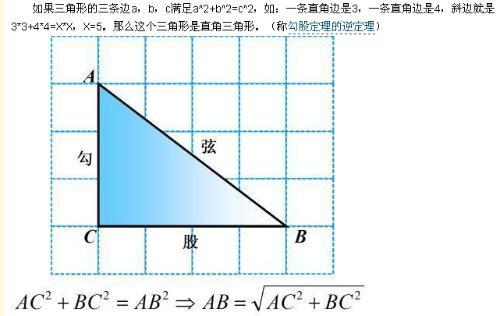
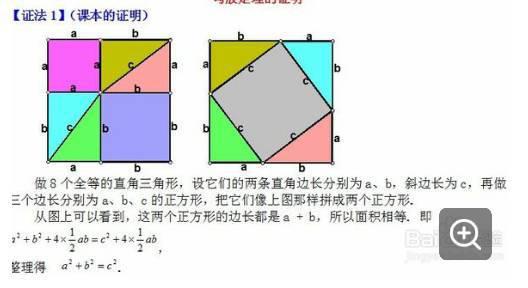
勾股定理是数学中的一个基本定理，它的副标题可以是“探究勾股定理的有趣应用”。在现代社会，勾股定理在各个领域都有着广泛的应用，因此了解和探究勾股定理的有趣应用也变得越来越重要。本文将介绍勾股定理在实际生活中的应用，以及一些有趣的例子。

应用一：测量建筑物高度

建筑物的高度是一个常见的测量量，而勾股定理可以用来测量建筑物的高度。在建筑测量中，常常需要测量建筑物的垂直高度，以便确定建筑物的面积和高度。通过勾股定理，可以轻松地计算出建筑物的高度。

应用二：计算跑道的长度

在田径场上，跑道的长度也是一个常见的测量量。勾股定理可以用来计算跑道的长度。通过测量起点和终点的位置，可以计算出跑道的长度。

应用三：测量篮球框的高度

篮球框的高度是一个常见的测量量，而勾股定理可以用来测量篮球框的高度。在篮球场地上，篮球框的高度也是一个非常重要的测量量。通过勾股定理，可以轻松地计算出篮球框的高度。

应用四：探究勾股定理的有趣应用

除了上述三个应用之外，勾股定理还可以在其他领域中发挥重要作用。例如，在物理学中，勾股定理可以用来计算物体的速度和加速度。在地理学中，勾股定理可以用来测量地球上两个地点之间的距离。

勾股定理是数学中的一个基本定理，它的应用非常广泛。了解和探究勾股定理的有趣应用，可以让我们更好地理解数学在现代社会中的重要性。