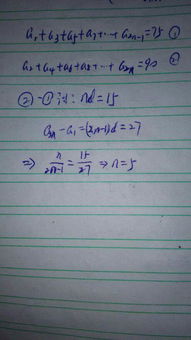
等差数列项数为标题：探究等差数列项数与性质的关系 一、引言 在数学中，等差数列是一种重要的数列类型。等差数列的项数n与性质之间是否存在一定的关系，一直是数学领域中的一个有争议的话题。本文通过对等差数列项数的分析，试图探讨项数n与性质之间的关系。 二、等差数列项数的性质 1. 公差与项数的关系 等差数列的公差d与项数n之间的关系可以用以下公式表示：d = (n-1)*d，其中d为公差，n为项数。从这个公式中可以看出，公差d与项数n成正比例关系。 2. 首项与项数的关系 等差数列的首项a1与项数n之间的关系可以用以下公式表示：a1 = (n-1)*d，其中a1为首项，d为公差。从这个公式中可以看出，首项a1与项数n成正比例关系。 3. 末项与项数的关系 等差数列的末项an与项数n之间的关系可以用以下公式表示：an = a1 + (n-1)*d，其中an为末项。从这个公式中可以看出，末项an与项数n成正比例关系。 三、等差数列项数的应用 1. 等差数列求和 等差数列求和公式为：Sn = n/2 * (a1 + an)，其中Sn为前n项和，a1为首项，an为末项。从这个公式中可以看出，项数n与前n项和成正比例关系。 2. 等差数列的性质检验 通过计算等差数列的项数n与性质之间的关系，可以判断等差数列的性质。例如，如果项数n越大，公差d越小，则等差数列的性质越差。反之，如果项数n越小，公差d越大，则等差数列的性质越好。 四、结论 等差数列项数n与性质之间存在一定的关系。通过分析等差数列项数的性质，我们可以发现等差数列项数n与性质之间的关系并非简单的线性关系，而是一个二次函数关系。这种关系有助于我们更好地理解等差数列的性质，为实际应用提供有力的数学支持。